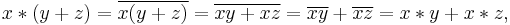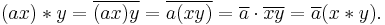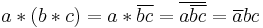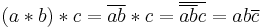Example of a non-associative algebra

This page presents and discusses an example of a non-associative division algebra over the real numbers.

The multiplication is defined by taking the complex conjugate of the usual multiplication: 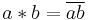$a*b=\overline{ab}$ . This is a commutative, non-associative division algebra of dimension 2 over the reals, and has no unit element.

Proof that 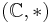$(\mathbb{C},*)$ is a division algebra

For a proof that $\mathbb{R}$ is a field, see real number. Then, the complex numbers themselves clearly form a vector space.

It remains to prove that the binary operation given above satisfies the requirements of a division algebra

(x + y)z = x z + y z;
x(y + z) = x y + x z;
(a x)y = a(x y); and
x(b y) = b(x y);

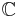for all scalars a and b in $\mathbb{R}$ and all vectors x, y, and z (also in $\mathbb{C}$ ).

For distributivity:

$x*(y%2Bz)=\overline{x(y%2Bz)}=\overline{xy%2Bxz}=\overline{xy}%2B\overline{xz}=x*y%2Bx*z,$

(similarly for right distributivity); and for the third and fourth requirements

$(ax)*y=\overline{(ax)y}=\overline{a(xy)}=\overline{a}\cdot\overline{xy}=\overline{a}(x*y).$

Non associativity of 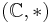$(\mathbb{C},*)$

$a * (b * c) = a * \overline{b c} = \overline{a \overline{b c}} = \overline{a} b c$

$(a * b) * c = \overline{a b} * c = \overline{\overline{a b} c} = a b \overline{c}$

So, if a, b, and c are all non-zero, and if a and c do not differ by a real multiple, 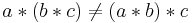$a * (b * c) \neq (a * b) * c$ .

Example of a non-associative algebra

Proof that is a division algebra

Non associativity of

Proof that $(\mathbb{C},*)$ is a division algebra

Non associativity of $(\mathbb{C},*)$